|
Abstract:
We prove a conjecture of Liu and Wang on the q-log-convexity
of the polynomial sequence 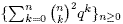 . By using Pieri's rule and the
Jacobi-Trudi identity for Schur functions, we obtain an expansion of a sum
of products of elementary symmetric functions in terms of Schur functions
with nonnegative coefficients. Then the principal specialization leads to the
q-log-convexity. We also prove that a technical condition of Liu and Wang
holds for the squares of the binomial coefficients. Hence we deduce that
the linear transformation with respect to the triangular array . By using Pieri's rule and the
Jacobi-Trudi identity for Schur functions, we obtain an expansion of a sum
of products of elementary symmetric functions in terms of Schur functions
with nonnegative coefficients. Then the principal specialization leads to the
q-log-convexity. We also prove that a technical condition of Liu and Wang
holds for the squares of the binomial coefficients. Hence we deduce that
the linear transformation with respect to the triangular array 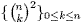 is
log-convexity preserving. is
log-convexity preserving.
AMS Classification: 05E05, 05E10
Keywords: q-log-convexity, Schur positivity, Pieri's rule, the Jacobi-Trudi
identity, principal specialization
Download: PDF
|