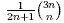Abstract:  The lattice polynomials L_i,j(x) are introduced by Hough and Shapiro as a weighted count of certain lattice paths from the origin to the point (i,j). In particular, L_{2n, n}(x) reduces to the generating function of the numbers T_n,k=, which can be viewed as a refinement of the 3-Catalan numbers T_n=. In this paper, we establish a correspondence between 12312-avoiding partial matchings and lattice paths, and we show that the weighted count of such partial matchings with respect to the number of crossings in a more general sense coincides with the lattice polynomials L_i,j(x). We also introduce a statistic on even trees, called the r-index, and show that the number of even trees with 2n edges and with r-index k equal to T_n,k.

  AMS Classification:  05A15

  Keywords:  lattice polynomial, 12312-avoiding partial matching, even tree.

  Download:   PDF