Abstract:  We present a systematic method for proving nonterminating basic hypergeometric identities. Assume that k is the summation index. By setting a parameter x to xqⁿ, we may find a recurrence relation of the summation by using the q-Zeilberger algorithm. This method applies to almost all nonterminating basic hypergeometric summation formulas in the book of Gasper and Rahman. Furthermore, by comparing the recursions and the limit values, we may verify many classical transformation formulas, including the Sears-Carlitz transformation, transformations of the very-well-poised series, the Rogers-Fine identity, and the limiting case of Watson's formula that implies the Rogers-Ramanujan identities.

  AMS Classification:  33D15; 33F10

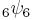  Keywords:  basic hypergeometric series, q-Zeilberger algorithm, Bailey's very-well-poised summation formula, Sears-Carlitz transformation, Rogers-Fine identity

  Download:   pdf