|
Abstract:
Let p(n) denote the partition function. Desalvo and Pak proved the log-concavity of p(n) for n>25 and the
inequality p(n-1)p(n)(1+1/n)>p(n)/p(n+1)
for n>1. Let r(n)=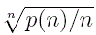 and Δ be the difference operator respect to n.
Desalvo and Pak pointed out that their approach to
proving the log-concavity of p(n) may be employed to prove
a conjecture of Sun on the log-convexity of
{r(n)}n≥61, as long as one finds an appropriate estimate of Δ2log r(n-1). In this paper, we obtain a lower bound for Δ2log r(n-1), leading to
a proof of this conjecture. From the log-convexity of {r(n)}n≥61} and and Δ be the difference operator respect to n.
Desalvo and Pak pointed out that their approach to
proving the log-concavity of p(n) may be employed to prove
a conjecture of Sun on the log-convexity of
{r(n)}n≥61, as long as one finds an appropriate estimate of Δ2log r(n-1). In this paper, we obtain a lower bound for Δ2log r(n-1), leading to
a proof of this conjecture. From the log-convexity of {r(n)}n≥61} and 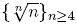 , we
are led to a proof of another conjecture of Sun on the log-convexity of , we
are led to a proof of another conjecture of Sun on the log-convexity of 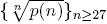 .
Furthermore, we show that .
Furthermore, we show that 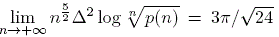 .
Finally, by finding an upper bound of Δ2log .
Finally, by finding an upper bound of Δ2log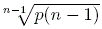 , we prove an inequality on the ratio , we prove an inequality on the ratio 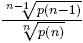 analogous to the above inequality on the ratio p(n-1)/p(n). analogous to the above inequality on the ratio p(n-1)/p(n).
AMS Classification: 05A20
Keywords: partition function, log-convex sequence, Hardy-Ramanujan-Rademacher
formula, Lehmer's error bound
Download: pdf
|
![]() and
and ![]()