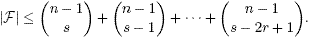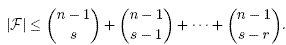Chen's paper - Lattice paths and the flagged Cauchy determiant

Abstract: Let p be a prime and let L = {l₁, l₂,..., l_s} and K = {k₁, k₂,... k_r} be two subsets of {0, 1, 2,..., p-1} satisfying max l_j < min k_i. We will prove the following results: If F = {F₁, F₂,..., F_m} is a family of subsets of [n]={1,2,..., n} such that |F_i∩F_j| (mod p) ∈ L for every pair i≠j and |F_i| (mod p) ∈ K for every 1 ≤ i ≤ m, then

If either K is a set of r consecutive integers or L={1,2,..., s}, then

We will also prove similar results which involve two families of subsets of [n]. These results improve the existing upper bounds substantially.

AMS Classification: 05A15, 05A18

Keywords: Erdös-Ko-Rado Theorem, Frankl-Ray-Chaudhuri-Wilson Theorems, Frankl-Füredi’s conjecture, Snevily's conjecture

Download: pdf