|
Abstract: Let p(n) denote the partition function. DeSalvo and Pak proved
that 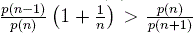 for n ≥ 2, as conjectured by Chen. Moreover,
they conjectured that a sharper inequality for n ≥ 2, as conjectured by Chen. Moreover,
they conjectured that a sharper inequality 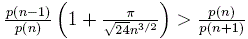 holds
for n ≥ 45. In this paper, we prove the conjecture of Desalvo and Pak
by giving an upper bound for -Δ2log p(n - 1), where Δ is the difference
operator with respect to n. We also show that for given r ≥ 1 and sufficiently
large n, (-1)Δrlog p(n) > 0. This is analogous to the positivity of finite
differences of the partition function. It was conjectured by Good and proved
by Gupta that for given r ≥ 1, Δrp(n) > 0 for sufficiently large n. holds
for n ≥ 45. In this paper, we prove the conjecture of Desalvo and Pak
by giving an upper bound for -Δ2log p(n - 1), where Δ is the difference
operator with respect to n. We also show that for given r ≥ 1 and sufficiently
large n, (-1)Δrlog p(n) > 0. This is analogous to the positivity of finite
differences of the partition function. It was conjectured by Good and proved
by Gupta that for given r ≥ 1, Δrp(n) > 0 for sufficiently large n.
AMS Classification: 05A20, 11B68
Keywords:
partition function, log-concavity, finite difference, the Lambert
W function, the Hardy-Ramanujan-Rademacher formula
Download: PDF
|